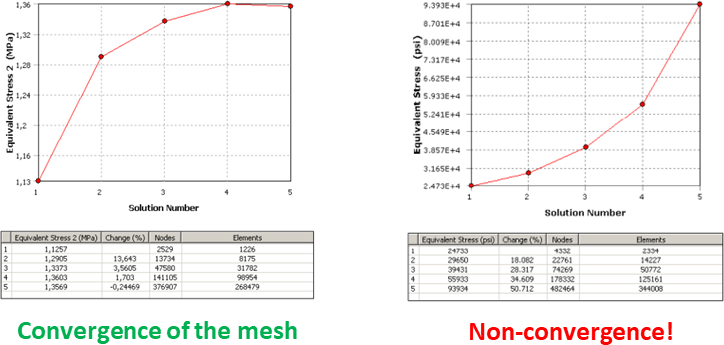
Maximum values of stress or strain, or alternatively peak stress or strain, could be potentially useful as a value to consider when comparing the biomechanical performance of different FEA models or when analyzing the same model under different scenarios or boundary conditions. However, peak stress and strain should not be considered like crazy because the value could be a numerical singularity, which is a well-known problem in FEA.

​The first option to avoid this awkward problem in your FEA model is avoid the application of punctual forces or boundary conditions using instead distributed options and avoid the perfect squares in the geometry rounding them. Of course, that this is not simple and in most of the cases you cannot avoid it. In this case, 

​However, if the aim of your FEA work is not intended to compare or use the values of stress and strain, but instead you want to compare qualitatively several models, a general stress pattern with these singularities may be accepted. Just be careful in displaying properly the distribution plots of stress and strain blurring the artificial high value. 

​Text modified from “Marcé-Nogué, J. (2020) Mandibular biomechanics as a key factor to understand diet in mammals”
​and “Marcé-Nogué, J. et al (2015) Improving mesh generation in Finite Element Analysis for functional morphology approaches”

Marcé‐Nogué, J., 2020. Mandibular biomechanics as a key factor to understand diet in mammals. In: Martin, T., W.V. Koenigswald (Eds.), Mammalian Teeth – Form and Function. Verlag Dr. Friedrich Pfeil, München, pp. 54–80. doi.org/10.23788/mammteeth.04
Marcé‐Nogué, J., de Esteban-Trivigno, S., Escrig, C., Gil, L., 2016. Accounting for differences in element size and homogeneity when comparing Finite Element models: Armadillos as a case study. Palaeontologia Electronica. 19, 1–22. https://doi.org/10.26879/609
Marcé‐Nogué, J., Fortuny, J., Gil, L., Sánchez, M., 2015. Improving mesh generation in Finite Element Analysis for functional morphology approaches. Spanish Journal of Palaeontology. 31, 117–132. hdl.handle.net/2117/82900
Tseng, Z.J., Flynn, J.J., 2018. Structure-function covariation with nonfeeding ecological variables influences evolution of feeding specialization in Carnivora. Science Advances. 4, eaao5441. doi.org/10.1126/sciadv.aao5441

Computational mechanics are able to reconstruct deformation, strain and stress in a digital structure after simulating a loading scenario by means of the finite element method and is has been extensively used in testing biomechanical hypothesis in functional morphology (Richmond et al., 2005). In particular, there are several different approaches that have been applied to analyse the results derived from mandibular mechanics to test theses hypotheses. While some works analyze stress results (Tseng et al., 2017) other focus on strain results (Panagiotopoulou et al., 2017). When using linear and elastic properties, it has been shown that both values are proportional and that the results of the distributions along the mandible are the same. This is due to the application of Hooke’s Law, which establishes a proportional relation between stress and strain. In fact, when linear and elastic material properties are assumed in a comparative analysis -comparing the performance of different mandibles from different taxa-, the effect of the elastic modulus of the material is irrelevant over stress patterns and strain patterns and comparative studies are allowed to be done without considering the real elastic materials properties (Gil et al., 2015). Therefore, most of the debate between the use of stress and strain is sterile when we are comparing the performance in different elastic models.

In this case, both stress and strain are accepted when comparing models below the fracture point, but, when we want to extrapolate these models to study fracture mechanics, a new debate is triggered: Is it stress or strain that causes failure? Probably the longest standing issue regarding failure criteria is whether they should be expressed in terms of stresses or in strains. In engineering, the most used form is the von Mises criterion expressed in terms of stress. Other criteria that are used are the maximum shear stress criterion (Tresca), the maximum normal stress criterion (Rankine) or the maximum normal strain criterion (Rankine). Despite the von Mises stress being a stress-designed criterion based on the maximum distortion of the strain energy, the stress-strain relations for isotropy can be used to convert the von Mises criterion in terms of stresses into a metric expressed in terms of strains. Therefore, it is usual to find in the literature the so-called “von Mises strain”. The transformation from stress to strain can be easily done using a simple mathematical procedure, but this does not eradicate the incontrovertible assumption that considers that all criteria can be switched from stress to strain (and vice versa). This is not always possible, especially when considering anisotropic material properties, but equally so for some isotropic cases. As an example, the maximum normal stress criterion and the maximum normal strain criterion take different forms when interconverted.

In my works, stress is taken as the fundamental form to be used when focusing on failure criteria. It is done because stress must be used if one wishes to have compatibility with fracture mechanics in the brittle range and with dislocation dynamics in the ductile range. Both theories require formulations in terms of stress. Moreover, in my comparative works in mandibles (Marcé‐Nogué, 2020), I understand that under equivalent loads, these stress patterns as a sign of the relative strength. According to the definition of strength in the Collins Dictionary “The strength of an object or material is its ability to be treated roughly, or to carry heavy weights, without being damaged or destroyed”. Therefore, it has sense that if we assume that more robust or stronger mandibles would be needed for processing harder food items, these mandibles should be expected to be weaker and, as a sign of strength, we use stress instead of strain to evaluate them, with higher stress indicating a weaker mandible.

On the other hand, strain has been shown valuable when comparing simulations results with experimental data (Bright and Rayfield, 2011), since strain gauges are commonly used in experimental settings. These electrical components experience changes in length as changes in resistance and this property can be used to measure strain on a bone surface and compare it with the FEA results obtained. Therefore, strain is the appropriate metric to compare in-vivo and in-silico data.

Text modified from “Marcé-Nogué, J. (2020) Mandibular biomechanics as a key factor to understand diet in mammals”.

Bright, J.A., Rayfield, E.J., 2011. Sensitivity and ex vivo validation of finite element models of the domestic pig cranium. Journal of Anatomy. 219, 456–471. https://doi.org/10.1111/j.1469-7580.2011.01408.x
Gil, L., Marcé‐Nogué, J., Sánchez, M., 2015. Insights into the controversy over materials data for the comparison of biomechanical performance in vertebrate. Palaeontologia Electronica. 287. https://doi.org/10.26879/509
Marcé‐Nogué, J., 2020. Mandibular biomechanics as a key factor to understand diet in mammals. In: Martin, T., W.V. Koenigswald (Eds.), Mammalian Teeth – Form and Function. Verlag Dr. Friedrich Pfeil, München, pp. 54–80.  https://doi.org/10.23788/mammteeth.04
Panagiotopoulou, O., Iriarte-Diaz, J., Wilshin, S., Dechow, P.C., Taylor, A.B., Mehari Abraha, H., Aljunid, S.F., Ross, C.F., 2017. In vivo bone strain and finite element modeling of a rhesus macaque mandible during mastication. Zoology. 124, 13–29. https://doi.org/10.1016/j.zool.2017.08.010
Richmond, B.G., Wright, B.W., Grosse, I., Dechow, P.C., Ross, C.F., Spencer, M.A., Strait, D.S., 2005. Finite element analysis in functional morphology. The Anatomical Record Part A: Discoveries in Molecular, Cellular, and Evolutionary Biology. 283A, 259–274. https://doi.org/10.1002/ar.a.20169
Tseng, Z.J., Su, D.F., Wang, X., White, S.C., Ji, X., 2017. Feeding capability in the extinct giant Siamogale melilutra and comparative mandibular biomechanics of living Lutrinae. Scientific Reports. 7, 15225. https://doi.org/10.1038/s41598-017-15391-9

During the months of the confinement due to the COVID-19 my colleagues from Transmitting Science asked me to record a short video to upload in the social networks. I decided to talk about the possibilities of Finite Element Analysis (FEA) in the field of vertebrates and when I mean possibilities, I mean different kind of elements, I mean different kind of geometries and, at the end of the street, different ways to create your FEA model. Because, of course, it is possible to use a tool from mechanical engineering to study the biomechanics of living and fossil vertebrates. It allows you for example to study locomotion or chewing and understand the evolution within their families. 

​But, what is Finite Element Analsys or FEA, which are the acronym of Finite Element Analysis? It is the matemathical way to solve problems of elasticity in complex geometries, so you can divide the geometry in tiny elements -but in a finite number- where the equations are easy to solve. Then, you can apply external forces in your model and understand how it deforms or how the inner forces are distributed inside the model. This method has been widely used in paleontology, antropology and functional morphology in general because now we can easily digitize the bony structures, so we can apply FEA in real geometries.  But, we cannot omit that we are creating models. So, Anderson et al. wrote in 2012 this sentence that today is still true:

"By definition, and in practice, models are not literal representations of reality but provide simplifications or substitutes of the events, scenarios or behaviours that are being studied or predicted. All models make assumptions. Therefore, we are creating models that maybe are not enough close to the reality but they can be very useful for our purpose."

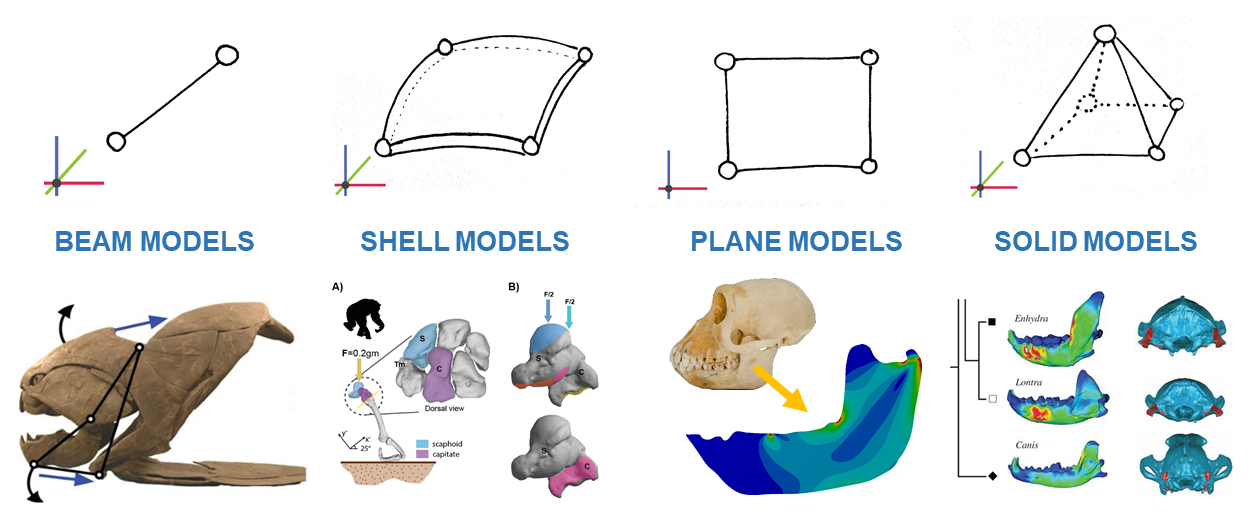
Following the idea of simplification that Anderson was underlying, there are different kind of elements that we can use when we are creating a FEA model. The use of some of this elements imply -of course- a simplification of the reality to a simple model.  So, let me introduce you this different kind of elements and their features.

1. The element BEAM: You use them when your geometry is a line and you are working in the 3D space or in 2D. You define them creating the mesh of the elements in this line and a defining a cross-section. You can see an example of their use in Anderson et al 2007 where they simplified the skull of a fish in a linkage of four beams.
2. The element SHELL: You use them when your geometry is a surface and you are working in the 3D space. You define them creating the mesh of the element in this surface and defining a constant thickness. You can see an example of their use in my work about carpal bones (Püschel et al. 2020) because they havve a tiny layer of cortical bone with cancellous bone inside.
3. The PLANE elements: You use them when your geometry can be simplified to a surface that can lye in a 2D plane. Be careful because this elements are not 2D elements, they are called PLANE elements because they use the equations of plane elasticity. The surface is lying in a plane, the forces you apply should lye in this plane and you mAst define a thickness. The thickness play a role in the results, so you cannot avoid it and, for this reason, you cannot use the term "2D" here. You can see an example of their use in models of mandibles. For example I used them to create FEA models of the mandible of several primates in Marcé-Nogué et al 2017.
4. The SOLID elements: You use them when your geometry is a volume and you are working in the 3D space. They are the most spread and the ones people is always using when you have a real geometry from a CT-Scan, photogrammetry or laser. You can see an example of their use in thi work of Jack Tseng (2016) where he modelled the mandibles of different carnivora in three-dimensions instead of other more simplified options. ​​

These are the options you have for adapting your geometries to your FEA model. But probably you are asking yourself two questions. The first one is: Which are the differences between shell elements and plane elements? Shell elements are not lying in a plane or, if yes, they allow forces that are not in the plane, like perpendicular forces. You can see this difference in the FEA models of the skull of several Temnospondyls (Fortuny et al. 2011) where the forces I applied are perpendicular to the flat surface of the skull.
And the second one: Probably you think that if you have a ct-scan and you create a FEA model with solid elements then you have a realistic model. I regret to inform you that this is the first step when creating FEA models and there is still a lot of decisions to make. And proabably, in most of them you will need to simplify your model because always remember that models are not literal representations of reality.

Anderson, P.S.L.L., Westneat, M.W., 2007. Feeding mechanics and bite force modelling of the skull of Dunkleosteus terrelli, an ancient apex predator. Biol. Lett. 3, 77–80. https://doi.org/10.1098/rsbl.2006.0569
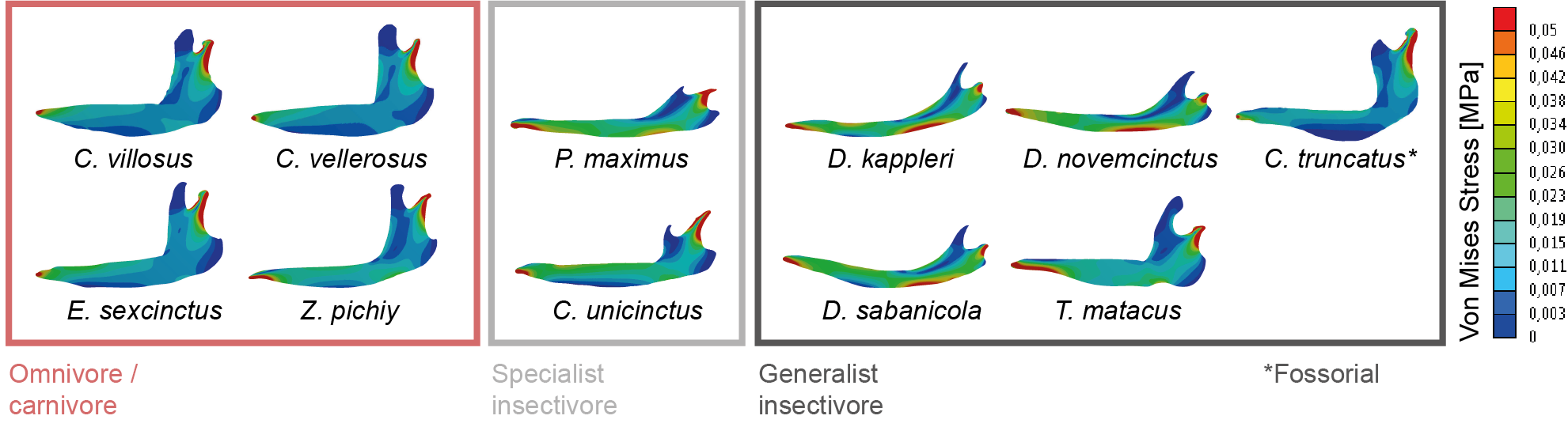
​Fortuny, J., Marcé-Nogué, J., DE Esteban-Trivigno, S., Gil, L., Galobart, Á., 2011. Temnospondyli bite club: ecomorphological patterns of the most diverse group of early tetrapods. J. Evol. Biol. 24, 2040–54. https://doi.org/10.1111/j.1420-9101.2011.02338.x
Marcé-Nogué, J., Püschel, T.A., Kaiser, T.M., 2017. A biomechanical approach to understand the ecomorphological relationship between primate mandibles and diet. Sci. Rep. 7, 8364. https://doi.org/10.1038/s41598-017-08161-0
​​Püschel, T.A., Marcé-Nogué, J., Chamberlain, A.T., Yoxall, A., Sellers, W.I., 2020. The biomechanical importance of the scaphoid-centrale fusion during simulated knuckle-walking and its implications for human locomotor evolution. Sci. Rep. 10, 3526. https://doi.org/10.1038/s41598-020-60590-6
​Tseng, Z.J., Grohé, C., Flynn, J.J., 2016. A unique feeding strategy of the extinct marine mammal Kolponomos : convergence on sabretooths and sea otters. Proc. R. Soc. B Biol. Sci. 283, 20160044. https://doi.org/10.1098/rspb.2016.0044

​In recent years, FEA models and the respective results have been compared in a predominantly qualitatively way, by comparing the stress or strain distributions. Visual comparison using only the stress or strain distribution of contour plots can be a good option when the number of models to is small and the results are distinctive enough between the analysed models (See Rayfield, 2007 for a review of FEA models in vertebrates). When we are solving a model using Finite Element Analysis, the results are obtained via a distribution map. These internal distributions of the forces -called stress- and ratios of deformation -strain- appear in the inner regions of the models due to the action of external forces. Computational biomechanics allow to model how different forces act on a biological structure like bones. The models of the bony structures are subdivided in small pieces called "elements" using a mesh where the equations are solved. Then, theoretical forces are applied to the model and the stress and strain values of each element are recorded and mapped in a coloured map called stress or strain distribution which enables a qualitative comparison between different models. Of course, this "coloured map" is related with numerical values. Specifically, with the values obtained from the solution in each element of the mesh representing stress or strain.

​​We published a work in 2015 “Finite Element Analysis of the Cingulata Jaw: An Ecomorphological Approach to Armadillo’s Diets” with several FEA models of armadillo mandibles (figure 1) in order to study the biomechanical performance during chewing and trying to relate it with the dietary preferences of each specie (Serrano-Fochs et al., 2015). Although quantifying stress or strain data at specific points of the model has been useful in previous ecomorphological analyses of the mammal mandible, in our work we could not find interesting patterns to be considered for analysing differences between models.

At this point, we decided to start developing new methods for quantifying the stress state from FEA of the armadillo mandibles. To analyse the stress values in a quantitative framework could be complicated, as these elements have different size in the same mesh. for this reason, we published recently the work "Accounting for differences in element size and homogeneity when comparing Finite Element models: Armadillos as a case study" (Marcé-Nogué et al., 2016). In this work we proposed a method to obtain the average mean and median of the distribution of these stresses in a Finite Element model weighting for the differences in elements size (mesh-weighted values). On the other hand, we proposed a procedure to check whether the meshes used to generate the elements provide accurate results to be used later in statistical analysis (quasi-ideal mesh). In other words, a consistent way to be sure that the stress values can be used as a proxy of the relative strength of vertebrate structures in a comparative framework for comparing the obtained mechanical results of different models between them. Figure 2A is an example of good practice. Boxplots of Von Mises stress distributions can be displayed only when Quasi-Ideal Meshes are assumed for all the different Cingulata mandibles analysed. It enables a qualitative comparison between species and, in this case, diets. The computation of average values or the display of stress is wrong unless all the elements of the mesh have the same size or have been corrected with the weight-meshed values. Mathematically speaking, the heterogeneity (or uniformity) in the size of the elements of the mesh can conditionate the results of the average value.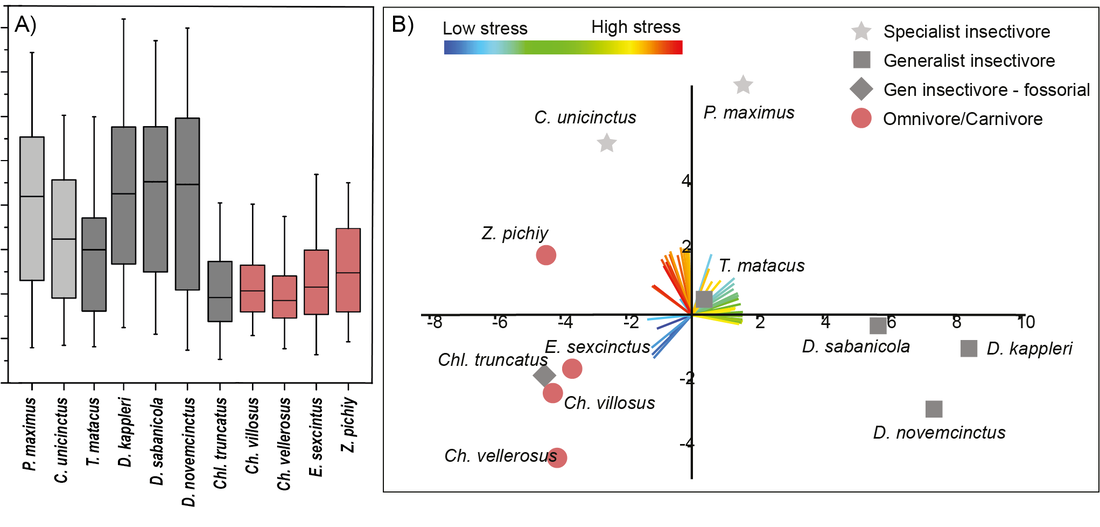

Recently in another work, we published "The intervals method: a new approach to analyse finite element outputs using multivariate statistics" (Marcé-Nogué et al., 2017a). This paper was a continuation of our previous works with armadillo mandibles where we were developing new methods to help the interpretation of FEA results. In this paper, we proposed a new method, named the intervals’ method, to analyse data from finite element models in a comparative multivariate framework. The method incorporates element volumes to provide an additional way of quantifying and comparing FEA results, thus avoiding the problems with the mesh. This method could allow for considerably more effective comparisons of finite element models, and maybe more precise distinction between dietary traits. As a case study once again, several armadillo mandibles were analysed, showing that the proposed method is useful to distinguish and characterise biomechanical differences related to diet/ecomorphology. The intervals’ method consists of generating a set of variables, each one defined by an interval of stress values. Each variable is expressed as a percentage of the area of the mandible occupied by those stress values. Afterwards these newly generated variables can be analysed using multivariate methods (see the biplot in figure 2B). Applying this novel method to the biological case study of whether armadillo mandibles differ according to dietary groups, we showed that the intervals’ method is a powerful tool to characterize biomechanical performance and how this relates to different diets. This allowed us to positively discriminate between specialist and generalist species and, moreover, something that it is very important when working with FEA: We show that the proposed approach is a useful methodology not affected by the characteristics of the finite element mesh. 

​Summarizing, these post-process methods are specially interesting because 1) open a new and imaginative way to compare large number of FEA models combined also with phylogenetic data (See Marcé-Nogué et al., 2017b in primates or Zhou et al., 2019 in ungulates) and 2) they can be used as an input data for the use of both supervised and non-supervised machine-learning (ML) algorithms. The use of ML is a powerful way that allow to classify sets of data as well as a predictor and has an incredible potential in inferring behaviours of extinct taxa. See Püschel et al., 2018 as an example of using the intervals method combined with ML algorithms.

​References