Do not be clumsy with the awkward problem of the peak value of stress

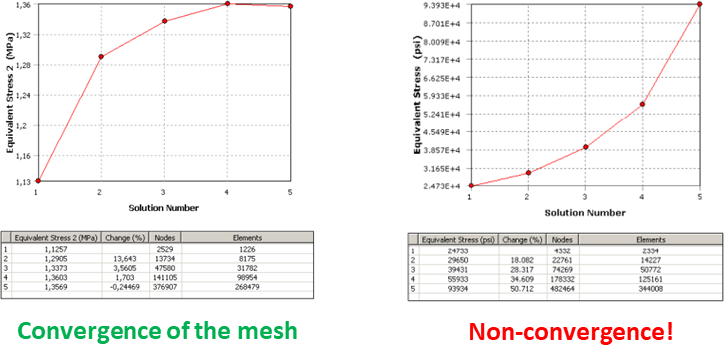
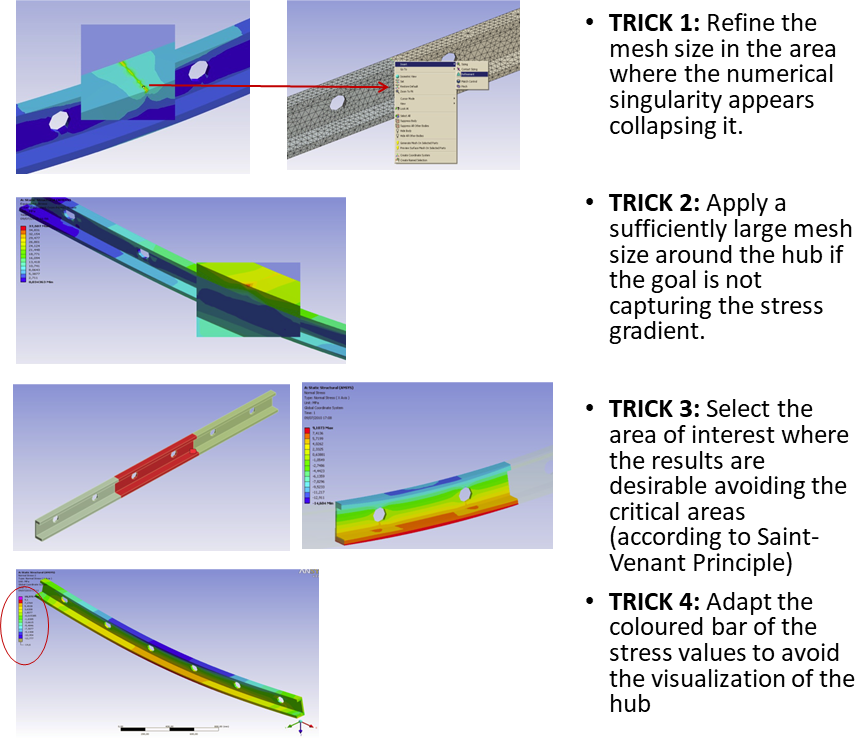
Maximum values of stress or strain, or alternatively peak stress or strain, could be potentially useful as a value to consider when comparing the biomechanical performance of different FEA models or when analyzing the same model under different scenarios or boundary conditions. However, peak stress and strain should not be considered like crazy because the value could be a numerical singularity, which is a well-known problem in FEA.

This singularity could be a consequence of a boundary condition or a perfect square within the geometry. A simply supported condition is an idealistic assumption because it creates a numerical effect that leads to the stress increasing without limit when the mesh is refined. In a similar way, the perfect square condition is also an idealistic assumption where a corner with zero radius in the original geometry creates a stress concentration that also leads the value to increase without limit when the mesh is refined. To avoid artificially high stress magnitudes, I do not recommend recording like crazy the maximum stress or strain values in the whole model, because maximum values could be the result of singular high yet unrealistic magnitudes. As some authors have warned previously, it may be difficult to assess the peak stresses of the model in the whole model. To detect a numerical singularity there is an easy trick which is performing a convergence test of the mesh (namely, reduce iteratively the size of the elements and solve the model to compare if the results are the same). Convergence tests will generate an artificial noise with a divergent value of stress towards infinite in the points where we have the singularity while the mesh is refined reducing the size of the elements.

Figure 1 - Typical plots from a convergence and a divergence of a five-step test of convergence of the mesh in a FEA model.

​The first option to avoid this awkward problem in your FEA model is avoid the application of punctual forces or boundary conditions using instead distributed options and avoid the perfect squares in the geometry rounding them. Of course, that this is not simple and in most of the cases you cannot avoid it. In this case, 

1. For example, this can be achieved by just studying the results obtained from an area of the model that is far enough from the artificially high magnitudes (which accomplish the Principle of Saint-Venant). This area of interest is suitable for convergence omitting the singularity and, in this case, the peak value can be recorded.
2. Another solution can be by adapting the mesh to avoid the visualization of this high value: Coarse meshes can avoid these extremely high stress values whereas very fine meshes can concentrate these high values in a very small region of the model. With this graphical solution, we cannot record the value of stress or strain, but we are removing the peak value of the distribution maps. Moreover, in both cases the stiffness of the model is not modified, and the displacement values can still be recorded.
3. Finally, other authors have suggested to exclude elements displaying the stress or strain values within the top 5% (Tseng and Flynn, 2018) or using a quasi-ideal mesh to record the percentiles where the values of stress are found (Marcé‐Nogué et al., 2016).

​However, if the aim of your FEA work is not intended to compare or use the values of stress and strain, but instead you want to compare qualitatively several models, a general stress pattern with these singularities may be accepted. Just be careful in displaying properly the distribution plots of stress and strain blurring the artificial high value. 

Figure 2 - Four tricks that you can use in your FEA models to avoid to see the artificial values of high stress in your FEA plots of distribution of stress (but not avoid to have!)

​Text modified from “Marcé-Nogué, J. (2020) Mandibular biomechanics as a key factor to understand diet in mammals”
​and “Marcé-Nogué, J. et al (2015) Improving mesh generation in Finite Element Analysis for functional morphology approaches”

References

Marcé‐Nogué, J., 2020. Mandibular biomechanics as a key factor to understand diet in mammals. In: Martin, T., W.V. Koenigswald (Eds.), Mammalian Teeth – Form and Function. Verlag Dr. Friedrich Pfeil, München, pp. 54–80. doi.org/10.23788/mammteeth.04
Marcé‐Nogué, J., de Esteban-Trivigno, S., Escrig, C., Gil, L., 2016. Accounting for differences in element size and homogeneity when comparing Finite Element models: Armadillos as a case study. Palaeontologia Electronica. 19, 1–22. https://doi.org/10.26879/609
Marcé‐Nogué, J., Fortuny, J., Gil, L., Sánchez, M., 2015. Improving mesh generation in Finite Element Analysis for functional morphology approaches. Spanish Journal of Palaeontology. 31, 117–132. hdl.handle.net/2117/82900
Tseng, Z.J., Flynn, J.J., 2018. Structure-function covariation with nonfeeding ecological variables influences evolution of feeding specialization in Carnivora. Science Advances. 4, eaao5441. doi.org/10.1126/sciadv.aao5441